7747. City Horizon
Farmer John
has taken his cows on a trip to the city! As the sun sets, the cows gaze at the
city horizon and observe the beautiful silhouettes formed by the rectangular
buildings.
The entire horizon is represented by a number line with n (1 ≤ n ≤ 40000) buildings.
Building is silhouette has a base that
spans locations ai through bi along
the horizon (1 ≤ ai < bi
≤ 109) and has height hi (1 ≤ hi ≤ 109).
Determine the area, in square units, of the aggregate silhouette formed by all n buildings.
Input. The first line contains a
single integer n. Each of the next n lines describes
building i with three
space-separated integers: ai, bi and hi.
Output. Print the total area, in
square units, of the silhouettes formed by all n buildings.
|
Sample input |
Sample output |
|
4 2 5 1 9 10 4 6 8 2 4 6 3 |
16 |
SOLUTION
sweeping
line
Algorithm analysis
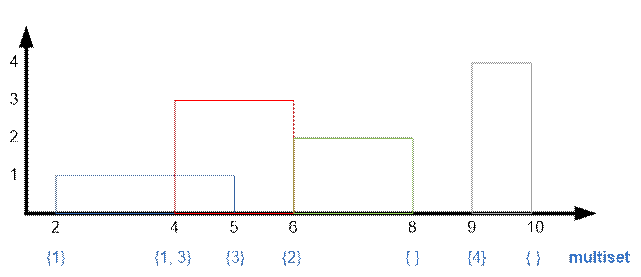
Lets sort the points the abscissas
of the beginning and the end of buildings in ascending order. With each
point store the information is it the beginning (type
= 0) or the end (type = 1) of the building, as well as the buildings height. Sequentially process the points from left to right.
In
the multiset s store the heights of
buildings that have already started but are not finished yet. Maintain the heights in the multiset in
descending order.
Let
at the moment we are at the point xi.
Let h be the largest
number in the multiset. This means that the current (at the interval [xi, xi+1]) tallest
building has a height h (that is not finished yet). Add the value (xi+1 xi) * h to the horizon area. If point xi
is the start of the building, then add the
corresponding height to the multiset. If point xi is the end of the building, then remove its height
from the multiset. The order of processing the starts
and the ends
of the buildings with the same abscissas
does not matter.
Example
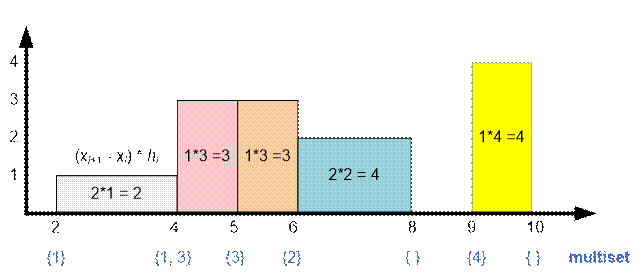
Algorithm realization
For a point, declare a structure node that will
store its abscissa x, information is it the start (type = 0) or the end (type =
1) of the segment, as well as the height h
of the corresponding building.
struct node
{
int x, type, h;
node(int x, int type, int h) : x(x), type(type), h(h) {};
};
Define a
comparator f for
points well sort
them by abscissas.
int f(node a, node b)
{
return a.x < b.x;
}
Declare an
array of points Event, as well as a
multiset s for
storing the heights of buildings
intersecting with the current abscissa of the sweeping
line.
vector<node> Event;
multiset<int,
greater<int> > s;
Read the
input data. Construct an array
of points.
scanf("%d",&n);
for(i = 0; i
< n; i++)
{
scanf("%d %d %d",&left,&right,&height);
Event.push_back(node(left,0,height));
Event.push_back(node(right,1,height));
}
Sort the array of points by non decreasing abscissas.
sort(Event.begin(),Event.end(),f);
In the variable res, compute the total area of the city
silhouette.
res = 0;
Move from
left to right along the points of the Event array. For each i
value of the for loop,
consider the interval (Event[i].x, Event[i + 1].x).
for (i = 0; i < Event.size() - 1; i++)
{
If point xi is
the start of the building, then add the
corresponding height to the multiset.
int h = Event[i].h;
if (Event[i].type == 0) s.insert(h);
If point xi is the end of the building, then
remove the corresponding height from the multiset.
else s.erase(s.find(h));
If stack is not empty, then between the points Event[i].x and Event[i + 1].x
there is a horizon line which height equals to the largest value in the multiset s,
namely the value *s.begin ().
if (!s.empty())
res += 1LL * *s.begin() *
(Event[i+1].x - Event[i].x);
}
Print the final area.
printf("%lld\n",res);
Algorithm realization segment tree
Lets compress
the abscissas of the buildings using the map mp (mp[2] =
1, mp[4] = 2, and so on). Build a segment tree [1..len], where len ≤
40000.
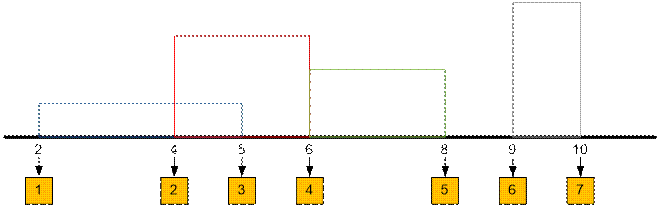
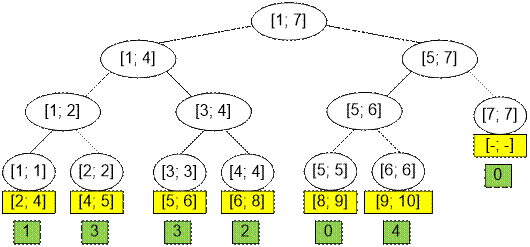
Each leaf of a segment
tree corresponds to one indivisible interval silhouette of a horizon. For example, vertex 1 corresponds to the
interval [2; 4], vertex 2 corresponds to the interval [4; 5]. Then segment [a,
b] is covered by the vertices [mp[a], mp[b] 1] of a segment tree. For example, the segment [2; 5] is covered by the
vertices [mp[2], mp [5] 1] = [1, 2].
For each building on the segment [ai,
bi] of height hi, increase by hi all values of the segment tree on the interval [mp[ai], mp[bi] 1]. When pushing the value at the vertex, maintain the maximum:
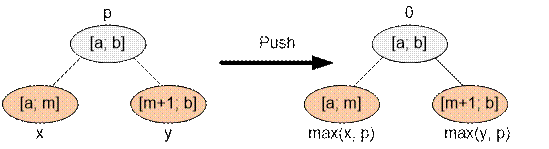
Lets push all
the vertex values to the leaves, after which the leaves will contain the silhouette
heights at the intervals. For example, the first leaf
corresponds to the segment [2; 4] and contains the value 1, the second leaf corresponds to the segment [4; 5] and contains the
value 3, and so on. The last node of the segment tree does not correspond to
any interval and is fictitious.
#include <cstdio>
#include <cstring>
#include <set>
#include <map>
#include <vector>
#include <algorithm>
#define MAX 80010
using namespace std;
int
SegTree[4*MAX];
vector<int>
a;
map<int,int> mp;
int i, n, l,
r, h, len;
long long res;
struct Building
{
int left, right, height;
} b[40010];
void Push(int Vertex, int
LeftPos, int Middle, int
RightPos)
{
if (SegTree[Vertex])
{
SegTree[2*Vertex] = max(SegTree[2*Vertex],SegTree[Vertex]);
SegTree[2*Vertex+1] = max(SegTree[2*Vertex+1],SegTree[Vertex]);
SegTree[Vertex] = 0;
}
}
void Add(int Vertex, int
LeftPos, int RightPos,
int
Left, int Right, int
x)
{
if (Left > Right) return;
if ((LeftPos == Left) && (RightPos == Right))
SegTree[Vertex] = max(SegTree[Vertex],x);
else
{
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
Add(2*Vertex, LeftPos, Middle, Left, min(Middle,Right), x);
Add(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right, x);
}
}
long long Count(int
Vertex, int LeftPos, int
RightPos)
{
if (LeftPos == RightPos)
return 1LL * SegTree[Vertex] * (a[LeftPos+1] -
a[LeftPos]);
else
{
int Middle =
(LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
return Count(2*Vertex, LeftPos, Middle) +
Count(2*Vertex+1, Middle+1, RightPos);
}
}
int main(void)
{
scanf("%d",&n);
memset(SegTree,0,sizeof(SegTree));
set<int> s;
for(i = 1; i <= n; i++)
{
scanf("%d %d %d",&b[i].left,&b[i].right,&b[i].height);
s.insert(b[i].left); s.insert(b[i].right);
}
len =
s.size(); a.resize(len+2);
copy(s.begin(),s.end(),a.begin()+1);
for(i = 1; i <= len; i++) mp[a[i]] = i;
for(i = 1; i <= n; i++)
Add(1,1,len,mp[b[i].left],mp[b[i].right]-1,b[i].height);
res =
Count(1,1,len);
printf("%lld\n",res);
return 0;
}